Вiдноснiсть швидкостей та перемiщень

Як вже зазначалося, рух та все, що з ним пов’язане – поняття вiдносне. Саме тому було введено поняття «система вiдлiку» та «тiло вiдлiку». Для того, щоб легко зрозуміти перехід від однієї системи відліку до іншої, розглянемо такий приклад. Микола рухається у рухомiй системi вiдлiку – в потязi зi швидкiстю та перемiщенням Миколи/потяга. Потяг (рухома система вiдлiку) має швидкiсть i перемiщення вiдносно нерухомої системи вiдлiку – землi з позначеннями потяга/землi. Тодi встановити рух Миколи вiдносно землi можна за допомогою суми цих двох векторiв.

Для подiбних задач рекомендуємо вам використовувати такий вид позначень, як зображено вище. Тоді ви не заплутаєтесь, розв’язуючи такі задачі.

Задача 3 ПЕТРО ТА РIКА ДЕСНА

Одного разу Петро вирiшив перепливти Десну. Вiн поплив перпендикулярно до течiї рiки та берегової лiнiї. Петро хотiв потрапити в ту точку, на яку взяв курс, але, нажаль, його ззнесла течія. На яку вiдстань вiд бажаної точки знесло Петра та який шлях вiн подолав? Ширина рiчки – $$50$$ м. Швидкiсть течiї рiчки – $$3$$ км/год. Зазвичай Петро плаває у басейнi зi швидкiстю $$4$$ км/год.

Дано: $$\upsilon_{п/р} = 4 \thinspace \text{км/год}, \ \upsilon_{п/з} = 3 \thinspace \text{км/год}, \ l = 50 \thinspace \text{м} = 0.05 \thinspace \text{км}$$

Знайти: $$ d, \ L$$

Схема Розв’язок Вiдповiдь ПриховатиРозв’язок.Для початку знайдемо, скiльки часу витратив Петро. \[t=\dfrac{|\thinspace \vec{S_{}}_{п/р} \thinspace|}{|\thinspace \vec{\upsilon}_{п/р} \thinspace|} = \dfrac{l}{\upsilon_{п/з}} = 0.05/4 = 0.0125 \thinspace (\text{год}) \]Зауважмо, що незалежно вiд швидкостi течiї, час, який витратив би Петро не змiнився. Це вiдбувається тому, що швидкiсть течiї в цьому випадку ніяк не впливає на швидкiсть з якою пливе Петро у перпендикулярному до течії напрямку. Змiнюється шлях, напрямок руху тiла та його швидкiсть, але не величина перпендикулярної компоненти.Вiдстань, на яку знесло Петра:\[ d = \upsilon_{\text{р/з}}t = 3 \cdot 0.0125 =0.0375 \thinspace \text{км} = 37.5 \thinspace \text{м}\]Шлях, який проплив Петро можна знайти двома способами:Знайти кінцеву швидкiсть Петра i помножити на час $$t$$: $$ \vec{\upsilon}_{п/з} =$$$$ \vec{\upsilon}_{п/р} + \vec{\upsilon}_{р/з} \Rightarrow $$ $$\upsilon_{п/з} =$$$$ \sqrt{(\vec{\upsilon}_{п/р})^2 + (\vec{\upsilon}_{р/з})^2} =$$$$ \sqrt{3^2 +4^2} =$$$$ 5 \thinspace (м/с) $$$$ L = \upsilon_{п/з}t = 5 \cdot 0.0125 = 0.0625 \thinspace \text{км} = 62.5 \thinspace \text{м}$$Через вiдомi модулi перемiщень (формула аналогiчна):$$L = \sqrt{l^2 + d^2} = \sqrt{50^2 +37.5^2}$$$$ = \sqrt{3906.25} = 62.5 \thinspace \text{м}$$Вiдповiдь.Шлях, який проплив Петро можна знайти двома способами:Знайти результуючу швидкiсть Петра i помножити на час $$t$$: $$ L = \upsilon_{п/з}t = 5 \cdot 0.0125 = 0.0625 \thinspace \text{км} = 62.5 \thinspace \text{м}$$Через вiдомi модулi перемiщень: $$L = \sqrt{l^2 + d^2} = \sqrt{50^2 +37.5^2}$$$$ = \sqrt{3906.25} = 62.5 \thinspace \text{м}$$

Озером перпендикулярно один до одного пливуть два човни зі швидкостями 3 м/с та 4 м/с відносно берега. Яка швидкість першого човна відносно другого? 5 0 3 1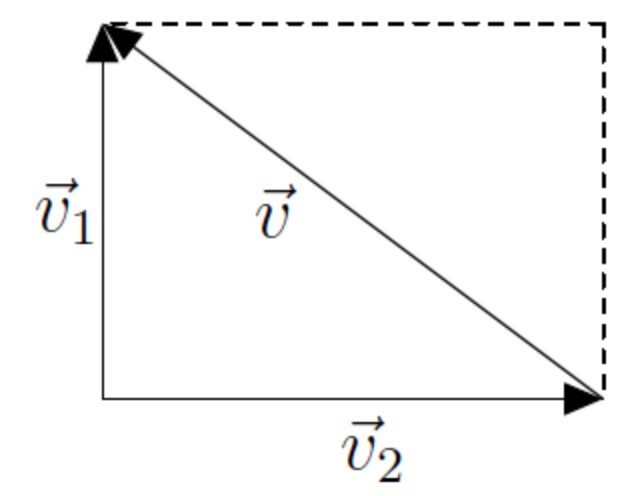

Нехай швидкість першого човна $$\vec{\upsilon}_1 = 3 \thinspace м/с$$, другого – $$\vec{\upsilon}_2 = 4 \thinspace м/с$$. Відносну швидкість човнів $$\vec{\upsilon}$$ можна знайти за правилом паралелограма для суми векторів $$\vec{\upsilon} = \vec{\upsilon}_1 + \vec{\upsilon}_2$$. Модуль (величину) цієї швидкості в цій задачі можна знайти за теоремою Піфагора, оскільки човни рухаються перпендикулярно один до одного:

$$|\thinspace \vec{\upsilon} \thinspace| = \sqrt{(\vec{\upsilon}_1)^2 + (\vec{\upsilon}_2)^2}$$

$$|\thinspace \vec{\upsilon} \thinspace| = \sqrt{3^2 + 4^2} = 5\thinspace м/с$$